คำอธิบายเพิ่มเติม

ทฤษฎีบทพีทาโกรัส กล่าวไว้ว่า
"ผลรวมของพื้นที่ของรูปสี่เหลี่ยมจัตุรัสบนด้านประชิดมุมฉากทั้งสอง จะเท่ากับ พื้นที่ของรูปสี่เหลี่ยมจัตุรัสบนด้านตรงข้ามมุมฉาก"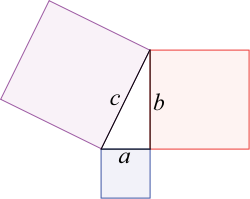

จากรูป จะสังเกตว่า ผลรวมของพื้นที่ของสี่เหลี่ยมสีน้ำเงินและสีแดง จะเท่ากับ พื้นที่ของสี่เหลี่ยมสีม่วง เราสามารถเขียนทฤษฎีบทนี้ให้อยู่ในรูป สมการ  c² = a² + b²  โดยที่ a และ b เป็นความยาวด้านประชิดมุมฉากทั้งสองของสามเหลี่ยมมุมฉาก และ c เป็นความยาวด้านตรงข้ามมุมฉาก

วิธีการพิสูจน์อีกแบบแสดงได้ดังรูปด้านล่าง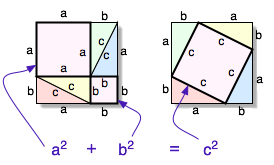


บทกลับของทฤษฎีบทปีทาโกรัส โดยกล่าวไว้ดังนี้
    "กำหนด a, b และ c เป็นจำนวนจริงบวกที่ a² + b² = c² จะมีสามเหลื่ยมมุมฉากหนึ่งรูปที่มีความยาวด้าน เป็นจำนวนสามจำนวนนั้น และด้านที่มีความยาว a และ b จะเป็นด้านประกอบมุมฉากของรูปสามเหลื่ยมนั้น"

บทกลับนี้ยังปรากฏอยู่ในหนังสือ Euclid's Elements ของ ยุคลิดด้วย โดยบทกลับนี้สามารถพิสูจน์ได้โดยใช้ กฎของโคไซน์ หรือตามการพิสูจน์ดังต่อไปนี้
    "กำหนดสามเหลี่ยม ABC มีด้านสามด้านที่มีความยาว a,b และ c และ a2 + b2 = c2 เราจะต้องพิสูจน์ว่ามุมระหว่าง a และ b เป็นมุมฉาก ดังนั้น เราจะสร้างสามเหลื่ยมมุมฉากที่มีความยาวของด้านประกอบมุมฉาก เป็น a และ b แต่จากทฤษฎีบทปีทาโกรัส เราจะได้ว่าด้านตรงข้ามมุมฉาก ของสามเหลื่ยมรูปที่สองก็จะมีค่าเท่ากับ c เนื่องจากสามเหลี่ยมทั้งสองรูปมีความยาวด้านเท่ากันทุกด้าน สามเหลี่ยมทั้งสองรูปจึงเท่ากันทุกประการแบบ "ด้าน-ด้าน-ด้าน" และต้องมีมุมขนาดเท่ากันทุกมุม ดังนั้นมุมที่ด้าน a และ b มาประกอบกัน จึงต้องเป็นมุมฉากด้วย"

จากบทพิสูจน์ของบทกลับของทฤษฎีบทปีทาโกรัส เราสามารถนำไปหาว่ารูปสามเหลี่ยมใด ๆ เป็นสามเหลี่ยมมุมแหลม, มุมฉาก หรือ มุมป้าน ได้ เมื่อกำหนดให้ c เป็นความยาวของด้านที่ยาวที่สุดในรูปสามเหลี่ยม
     ถ้า a² + b² = c²   สามเหลี่ยมนั้นจะเป็นสามเหลี่ยมมุมฉาก
     ถ้า a² + b² < c²   สามเหลี่ยมนั้นจะเป็นสามเหลี่ยมมุมแหลม
     ถ้า a² + b² > c²   สามเหลี่ยมนั้นจะเป็นสามเหลี่ยมมุมป้าน


แหล่งที่มา : วิกิพีเดีย