งาน
สมาชิกเลขที่12053 | 27 เม.ย. 53
2.9K views
จำนวนตรรกยะ (Rational Number) คือ จำนวนที่สามารถเขียนในรูปเศษส่วน a/b เมื่อ a และ b เป็นจำนวนเต็มโดยที่ b ¹ 0 จำนวนตรรกยะ จำแนกได้เป็น 3 ประเภทใหญ่ ๆ คือ
1. จำนวนเต็ม (Integer)
2. เศษส่วน (Fraction)
3. ทศนิยม (Repeating decimal)
จำนวนอตรรกยะ (irrational Number) คือ จำนวนที่ไม่สามารถเขียนในรูปเศษส่วน a/b เมื่อ a และ b เป็นจำนวนเต็มโดยที่ b ¹ 0 หรือจำนวนอตรรกยะคือ จำนวนที่ไม่ใช่จำนวนตรรกยะนั่นเอง จำนวนอตรรกยะ จำแนกได้เป็น 2 ประเภทใหญ่ใหญ่คือ
1. จำนวนติดกรณ์บางจำนวน เช่น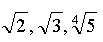 เป็นต้น
เป็นต้น
2. จำนวนทศนิยมไม่ซ้ำเช่น 5.18118168473465
หมายเหตุ p ซึ่งประมาณได้ด้วย 22/7 แต่จริงๆ แล้ว p เป็นเลขอตรรกยะ
สิ่ง ที่ควรทราบ

จำนวนจริงทุกจำนวนสามารถแทนได้ด้วยจุดบนเส้นจำนวน
ราก ที่สอง(Square root )
นิยาม กำหนดให้ a แทนจำนวนจริงบวกใด ๆ หรือ ศูนย์ รากที่สองของ a คือ จำนวนจริงที่ยกกำลังสองแล้วได้ a
1. ถ้า a เป็นจำนวนจริงบวก รากที่สองของ a มี 2 ราก คือ
2. ถ้า a = 0 รากที่สองของ a คือ 0
การหารากที่สอง
1. การหารากที่สองโดยแยกตัวประกอบ
ตัวอย่างที่ 1 จงหา รากที่สองของ 64
วิธีทำ 64 = 2 x2x2x2x2x2 = 8 x 8 = 82
หรือ 64 = (-8) x (-8) = (-8) 2
ดังนั้น รากที่สองของ 64 คือ 8 และ -8
2. การหารากที่สองของเลขจำนวนเต็มบวกโดยการตั้งหาร

3. การหารรากที่สองของทศนิยม โดยการตั้งหาร
มีหลักเหมือนการหารากที่สองของเลขจำนวนเต็มทุกประการ จะแตกต่างกันก็แต่เพียงการแบ่งเลขเป็นชุด ๆ หลังจุดทศนิยมจะแบ่งจากซ้ายไปขวา (โดยเริ่มจากจุดทศนิยม) ครั้งละ 2 หลัก โดยมีเครื่องหมาย , คั่นเช่นกัน ลองทำดูนะคะ เช่น จงหาราที่สองของ 10.58 = 3.2527 เป็นต้น
รากที่ 3 (Cube root)
นิยาม ให้ a แทนจำนวนจริงใด ๆ รากที่สามของ a คือ จำนวนจริงที่ยกกำลังสามแล้วได้ a เขียนแทนด้วยสัญลักษณ์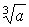
หมายเหตุ : รากที่สามของจำนวนจริงใด ๆ จะเป็นจำนวนตรรกยะหรือ
อตรรกยะอย่างใดอย่าง หนึ่งเท่านั้น
คุณสมบัติของจำนวนเต็ม
1. จำนวนนับ (counting number) คือ จำนวนที่เราใช้นับสิ่งของต่าง ๆ เริ่มตั้งแต่ 1, 2 , 3 , … หรือเรียกอีกอย่างหนึ่งว่า จำนวนธรรมชาติ (natural number) จำนวนนับจำแนกได้ 2 กลุ่มคือ จำนวนคู่ กับจำนวนคี่
1.1 จำนวนคู่ (odd number) คือ จำนวนนับที่มี 2 เป็นตัวประกอบ (หาร 2 ลงตัว) เช่น 2, 4 , 6 , 8 ,…. เป็นต้น
1.2 จำนวนคี่ (even number) คือ จำนวนนับอื่นที่ไม่ใช่จำนวนคู่(หาร 2 ไม่ลงตัว) เช่น 1 ,3 , 5 , 7 …เป็นต้น
2. ตัวประกอบ (factor) คือ จำนวนนับที่หารจำนวนนับนั้นได้ลงตัว
เช่น 2 เป็นตัวประกอบของ 4 เพราะ 2 หาร 4 ได้ลงตัว
5 เป็นตัวประกอบของ 15 เพราะ 5 หาร 15 ได้ลงตัว
3. จำนวนเฉพาะ (prime number) คือ จำนวนนับที่มากกว่า 1 และมีตัวประกอบเพียง 2 ตัวคือ 1 และตัวมันเอง เช่น 2, 3 , 5 , 7 , 11 ,…
4. การแยกตัวประกอบ (factoring) คือ ประโยคที่แสดงการเขียนจำนวนนั้น ๆ ในรูปการคูณของตัวประกอบเฉพาะ
การแยกตัวประกอบนิยมใช้มี 3 วิธีคือ
4.1 ใช้แผนภาพต้นไม้ (treediagram) แล้วนำตัวประกอบเฉพาะทุกตัวที่อยู่ปลายกิ่งไม้ทุก ๆ กิ่งมาคูณกัน เช่น
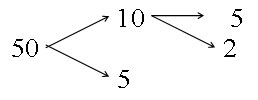
ดังนั้น 50 = 5 x 2 x 5
4.2 ใช้การเขียนในรูปผลคูณของตัวประกอบร่วม (แนวคิดจากวิธีที่ 1) เช่น 50 = 5 x 10 = 5 x 2 x 5
4.3 ใช้วิธีหารสั้นโดยใช้จำนวนเฉพาะที่เป็นตัวประกอบของจำนวนนั้น ๆ มาหาร เช่น จงแยกตัวประกอบของ 1155
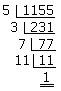
ดังนั้น 1155 = 5 x 3 x 7 x 11
5. ตัวหาร่วมมาก (ห.ร.ม.)(greatest common divisor) คือ ตัวประกอบร่วมที่มีค่ามากที่สุดของจำนวนนับเหล่านั้นนั่นเอง
ตัวอย่าง ค่ายลูกเสือแห่งหนึ่งมีลูกเสือมาพักแรม 3 กอง กองที่ 1 มี 45 คน กองที่ 2 มี 60 คน กองที่ 3 มี 90 คน ถ้าจะแบ่งลูกเสือในแต่ละกองออกเป็นหมู่ ๆ ให้แต่ละหมู่มีสมาชิกเท่ากันและมากที่สุด จะต้องแบ่งลูกเสือออกเป็นหมู่ละกี่คน
วิธีทำ จำนวนลูกเสือมากที่สุดคือ การหา ห.ร.ม. ของ 45 , 60 และ 90
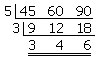
ดังนั้น ห.ร.ม. ของ 45 , 60 และ 90 คือ 5 x 3 = 15
6. ตัวคูณร่วม น้อย (ค.ร.น.) (least common multiple ) คือ ตัวคูณร่วมน้อยที่สุดของจำนวนนับเหล่านั้นนั่นเอง
ตัวอย่าง จงหา ค.ร.น. ของ 9, 30 และ 40
วิธีทำ
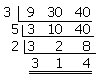
ดังนั้น ค.ร.น. ของ 9 , 30 และ 40 คือ 3 x 5 x 2 x 3 x 4 = 360
ความ สัมพันธ์ของ ค.ร.น. และ ห.ร.ม. คือ ถ้า A เป็น ค.ร.น. ของ x กับ y และ B เป็น ห.ร.ม. ของ x กับ y จะได้ว่า AxB = (x)(y)
เช่น ค.ร.น. ของ 8 และ 12 คือ 24 และ ห.ร.ม. ของ 8 และ 12 คือ 4
จะได้ว่า 24x4 = 8x12 96 = 96
1. จำนวนเต็ม (Integer)
2. เศษส่วน (Fraction)
3. ทศนิยม (Repeating decimal)
จำนวนอตรรกยะ (irrational Number) คือ จำนวนที่ไม่สามารถเขียนในรูปเศษส่วน a/b เมื่อ a และ b เป็นจำนวนเต็มโดยที่ b ¹ 0 หรือจำนวนอตรรกยะคือ จำนวนที่ไม่ใช่จำนวนตรรกยะนั่นเอง จำนวนอตรรกยะ จำแนกได้เป็น 2 ประเภทใหญ่ใหญ่คือ
1. จำนวนติดกรณ์บางจำนวน เช่น
2. จำนวนทศนิยมไม่ซ้ำเช่น 5.18118168473465
หมายเหตุ p ซึ่งประมาณได้ด้วย 22/7 แต่จริงๆ แล้ว p เป็นเลขอตรรกยะ
สิ่ง ที่ควรทราบ

จำนวนจริงทุกจำนวนสามารถแทนได้ด้วยจุดบนเส้นจำนวน
ราก ที่สอง(Square root )
นิยาม กำหนดให้ a แทนจำนวนจริงบวกใด ๆ หรือ ศูนย์ รากที่สองของ a คือ จำนวนจริงที่ยกกำลังสองแล้วได้ a
1. ถ้า a เป็นจำนวนจริงบวก รากที่สองของ a มี 2 ราก คือ
2. ถ้า a = 0 รากที่สองของ a คือ 0
การหารากที่สอง
1. การหารากที่สองโดยแยกตัวประกอบ
ตัวอย่างที่ 1 จงหา รากที่สองของ 64
วิธีทำ 64 = 2 x2x2x2x2x2 = 8 x 8 = 82
หรือ 64 = (-8) x (-8) = (-8) 2
ดังนั้น รากที่สองของ 64 คือ 8 และ -8
2. การหารากที่สองของเลขจำนวนเต็มบวกโดยการตั้งหาร

3. การหารรากที่สองของทศนิยม โดยการตั้งหาร
มีหลักเหมือนการหารากที่สองของเลขจำนวนเต็มทุกประการ จะแตกต่างกันก็แต่เพียงการแบ่งเลขเป็นชุด ๆ หลังจุดทศนิยมจะแบ่งจากซ้ายไปขวา (โดยเริ่มจากจุดทศนิยม) ครั้งละ 2 หลัก โดยมีเครื่องหมาย , คั่นเช่นกัน ลองทำดูนะคะ เช่น จงหาราที่สองของ 10.58 = 3.2527 เป็นต้น
รากที่ 3 (Cube root)
นิยาม ให้ a แทนจำนวนจริงใด ๆ รากที่สามของ a คือ จำนวนจริงที่ยกกำลังสามแล้วได้ a เขียนแทนด้วยสัญลักษณ์
หมายเหตุ : รากที่สามของจำนวนจริงใด ๆ จะเป็นจำนวนตรรกยะหรือ
อตรรกยะอย่างใดอย่าง หนึ่งเท่านั้น
คุณสมบัติของจำนวนเต็ม
1. จำนวนนับ (counting number) คือ จำนวนที่เราใช้นับสิ่งของต่าง ๆ เริ่มตั้งแต่ 1, 2 , 3 , … หรือเรียกอีกอย่างหนึ่งว่า จำนวนธรรมชาติ (natural number) จำนวนนับจำแนกได้ 2 กลุ่มคือ จำนวนคู่ กับจำนวนคี่
1.1 จำนวนคู่ (odd number) คือ จำนวนนับที่มี 2 เป็นตัวประกอบ (หาร 2 ลงตัว) เช่น 2, 4 , 6 , 8 ,…. เป็นต้น
1.2 จำนวนคี่ (even number) คือ จำนวนนับอื่นที่ไม่ใช่จำนวนคู่(หาร 2 ไม่ลงตัว) เช่น 1 ,3 , 5 , 7 …เป็นต้น
2. ตัวประกอบ (factor) คือ จำนวนนับที่หารจำนวนนับนั้นได้ลงตัว
เช่น 2 เป็นตัวประกอบของ 4 เพราะ 2 หาร 4 ได้ลงตัว
5 เป็นตัวประกอบของ 15 เพราะ 5 หาร 15 ได้ลงตัว
3. จำนวนเฉพาะ (prime number) คือ จำนวนนับที่มากกว่า 1 และมีตัวประกอบเพียง 2 ตัวคือ 1 และตัวมันเอง เช่น 2, 3 , 5 , 7 , 11 ,…
4. การแยกตัวประกอบ (factoring) คือ ประโยคที่แสดงการเขียนจำนวนนั้น ๆ ในรูปการคูณของตัวประกอบเฉพาะ
การแยกตัวประกอบนิยมใช้มี 3 วิธีคือ
4.1 ใช้แผนภาพต้นไม้ (treediagram) แล้วนำตัวประกอบเฉพาะทุกตัวที่อยู่ปลายกิ่งไม้ทุก ๆ กิ่งมาคูณกัน เช่น

ดังนั้น 50 = 5 x 2 x 5
4.2 ใช้การเขียนในรูปผลคูณของตัวประกอบร่วม (แนวคิดจากวิธีที่ 1) เช่น 50 = 5 x 10 = 5 x 2 x 5
4.3 ใช้วิธีหารสั้นโดยใช้จำนวนเฉพาะที่เป็นตัวประกอบของจำนวนนั้น ๆ มาหาร เช่น จงแยกตัวประกอบของ 1155
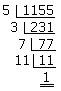
ดังนั้น 1155 = 5 x 3 x 7 x 11
5. ตัวหาร่วมมาก (ห.ร.ม.)(greatest common divisor) คือ ตัวประกอบร่วมที่มีค่ามากที่สุดของจำนวนนับเหล่านั้นนั่นเอง
ตัวอย่าง ค่ายลูกเสือแห่งหนึ่งมีลูกเสือมาพักแรม 3 กอง กองที่ 1 มี 45 คน กองที่ 2 มี 60 คน กองที่ 3 มี 90 คน ถ้าจะแบ่งลูกเสือในแต่ละกองออกเป็นหมู่ ๆ ให้แต่ละหมู่มีสมาชิกเท่ากันและมากที่สุด จะต้องแบ่งลูกเสือออกเป็นหมู่ละกี่คน
วิธีทำ จำนวนลูกเสือมากที่สุดคือ การหา ห.ร.ม. ของ 45 , 60 และ 90

ดังนั้น ห.ร.ม. ของ 45 , 60 และ 90 คือ 5 x 3 = 15
6. ตัวคูณร่วม น้อย (ค.ร.น.) (least common multiple ) คือ ตัวคูณร่วมน้อยที่สุดของจำนวนนับเหล่านั้นนั่นเอง
ตัวอย่าง จงหา ค.ร.น. ของ 9, 30 และ 40
วิธีทำ

ดังนั้น ค.ร.น. ของ 9 , 30 และ 40 คือ 3 x 5 x 2 x 3 x 4 = 360
ความ สัมพันธ์ของ ค.ร.น. และ ห.ร.ม. คือ ถ้า A เป็น ค.ร.น. ของ x กับ y และ B เป็น ห.ร.ม. ของ x กับ y จะได้ว่า AxB = (x)(y)
เช่น ค.ร.น. ของ 8 และ 12 คือ 24 และ ห.ร.ม. ของ 8 และ 12 คือ 4
จะได้ว่า 24x4 = 8x12 96 = 96

