1,142 Views
Favorite
ระบบการเขียนตัวเลขแทนจำนวนที่ใช้กันในปัจจุบัน เป็นระบบฐานสิบ และตัวเลขที่ใช้กันเป็นสากลนี้เรียกว่า ตัวเลขฮินดูอารบิก
ในระบบฐานสิบ มีสัญลักษณ์ที่ใช้เขียนแทนจำนวนสิบตัว คือ 1, 2, 3, 4, 5, 6, 7, 8, 9 และ 0 เรานิยมนับเป็นหมู่ หมู่ละสิบ เมื่อครบสิบในหลักใดจะทดขึ้นเป็นหนึ่งหน่วยของหลักที่ถัดไปทางซ้ายมือ ซึ่งมีชื่อตามลำดับจากน้อยไปมากว่า หลักหน่วย หลักสิบ หลักร้อย หลักพัน หลักหมื่น หลักแสน หลักล้าน เราอาจเขียนแผนผังของข้อตกลงในระบบฐานสิบได้ดังนี้
และ อาจเขียนแผนผังของข้อตกลงในระบบฐานสิบในรูปตาราง โดยแสดงค่าประจำ ตำแหน่งเทียบกับหลักได้ดังนี้
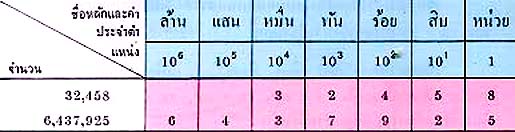
32,458 = (3x10^4) + (2x10^3) + (4x10^2) + (5x10) + (8x1)
6,437,925 = (6x10^6) + (4x10^5) + (3x10^4) + (7x10^3) + (9x10^2) + (2x10) + (5x1)
ดังนั้นถ้า N แทนจำนวนใดๆ ในระบบฐานสิบ เราอาจเขียนได้ว่า
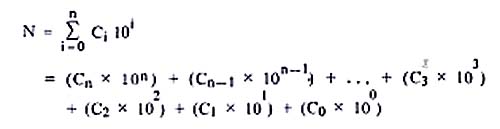
โดยที่ Co, C1, C2,...,Cn เป็นตัวเลขในหลักหน่วย หลักสิบ หลักร้อย หลักพันเรื่อยๆ ขึ้นไปตามลำดับ ตัวเลขเหล่านี้ เป็นตัวเลขใดตัวเลขหนึ่งใน บรรดา 1, 2, 3, 4, 5, 6, 7, 8, 9 และ 0
