

 10,422 Views
10,422 Views
คนสมัยโบราณมีวิธีตอบคำถามที่ว่า "เท่าไร" ได้ ถึงแม้ว่าเขาจะยังไม่มีคำที่ใช้เรียกจำนวน และยังไม่มีสัญลักษณ์ ที่เขียนแทนจำนวน

เขาใช้วิธีขีดรอยบนกิ่งไม้ หรือใช้กิ่งไม้เล็กๆ แทนสิ่งที่จะต้องนับทีละสิ่ง
ต่อมาเมื่อคนรู้จักบันทึกเรื่องราวเพื่อช่วยความจำ เขาจึงเขียนสัญลักษณ์ขึ้นสำหรับแทนจำนวน

ชาวบาบิโลนบันทึกเรื่องราวลงบนแผ่นดินเหนียวสัญลักษณ์ที่เขียนแทนจำนวนจึงมีรูปร่าง ดังนี้
สัญลักษณ์ที่เขียนแทนจำนวน เรียกว่า ตัวเลข ตัวเลขที่ใช้ในปัจจุบันทั่วโลก เป็นตัวเลขฮินดูอารบิกได้แก่ 1,2,3,4,5,6,7,8,9,0 ตัวเลขฮินดูอารบิกนี้ชาวฮินดูเป็นผู้คิด ชาวอาหรับเป็นผู้นำไปเผยแพร่
คนไทยมีตัวเลขไทย ในสมัยพ่อขุนรามคำแหงมหาราช และ ได้ดัดแปลงเพิ่มเติมจนถึงปัจจุบัน ปรากฏตามหลักฐานดังนี้

ตัวอย่างของตัวเลขชาติต่างๆ ที่แทนจำนวนแมลง ๑๕ ตัวในขวดโหลใบนี้

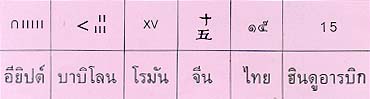
ตัวเลขอียิปต์
ในสมัยโบราณ อียิปต์เป็นชาติที่เจริญรุ่งเรือง ทางด้านศิลปวิทยาการ ก่อนชาติอื่นๆ ชาวอียิปต์รู้จักบันทึกจำนวน โดยใช้สัญลักษณ์ต่างๆ ดังต่อไปนี้

การเขียนสัญลักษณ์แทนจำนวนของชาวอียิปต์ ใช้วิธีรวมค่าของสัญลักษณ์เหล่านั้น ไม่คำนึงถึงตำแหน่งของสัญลักษณ์ ดังนั้น จำนวนเดียวกัน อาจจะเขียนสัญลักษณ์สลับที่เป็นแบบต่างๆ ได้

ตัวเลขบาบิโลน
เมื่อประมาณ ๓,๐๐๐ ปีก่อนคริสต์ศักราช ประเทศบาบิโลนเนียตั้งอยู่ทางตะวันออกของทะเลเมดิเตอร์เรเนียน ปัจจุบัน เป็นที่ตั้งของประเทศซีเรีย และ เลบานอน ในกลางศตวรรษที่ ๑๙ นักโบราณคดีได้ขุดพบแผ่นอิฐมากกว่าห้าหมื่นแผ่น ใกล้ๆ กับเมืองนิปเปอร์ (Nippur) และ ได้นำแผ่นอิฐเหล่านี้ไปเก็บไว้ในพิพิธภัณฑ์ใหญ่ๆ ที่กรุงปารีส ประเทศฝรั่งเศส ที่กรุงลอนดอน ประเทศอังกฤษ และ กรุงเบอร์ลิน ประเทศเยอรมนี รวมทั้งสถานที่แสดงวัตถุโบราณที่เยล โคลัมเบีย และ ที่มหาวิทยาลัยเพนซิลวาเนียในสหรัฐอเมริกา จากแผ่นอิฐ ทำให้ทราบเรื่องราวของชาวบาบิโลน

ชาวบาบิโลนถือตำแหน่งของสัญลักษณ์เป็นสำคัญ ถ้าสลับที่สัญลักษณ์ จะทำให้ได้จำนวนที่มีค่าต่างกัน ดังเช่น
<|| ไม่เท่ากับ |<| จำนวนแรกแทนสิบสอง จำนวนหลังแทนเจ็ดสิบเอ็ด
ต่อมาเมื่อมีความจำเป็นต้องแสดงจำนวนที่ใหญ่ขึ้น เขาจะใช้สัญลักษณ์นี้เขียนเป็นกลุ่มใหม่ โดยนำกลุ่มนี้ ไปไว้ทางซ้าย ของกลุ่มเดิม ที่แทนจำนวนสิบกับหนึ่ง และ กำหนดให้สัญลักษณ์ในกลุ่มใหม่ มีค่าเป็นหกสิบเท่าของจำนวนในกลุ่มนี้เช่น

ตำแหน่งของสัญลักษณ์ที่ชาวบาบิโลนกำหนดไว้ จะประกอบด้วยหลักหน่วยนับได้ตั้งแต่ หนึ่งถึงห้าสิบเก้า เขียนเป็นกลุ่ม อยู่ทางขวามือสุด กลุ่มที่สองซึ่งอยู่ถัดไปทางซ้าย จะเป็นหลักหกสิบ ซึ่งจะมีค่าเป็นหกสิบเท่าของจำนวนในหลักนั้น กลุ่มที่สาม กลุ่มที่สี่ และ กลุ่มต่อไป ที่อยู่ถัดไปทางซ้ายก็จะเป็นหลักหกสิบกำลังสอง, หลักหกสิบกำลังสาม,... ไปตามลำดับ เช่น
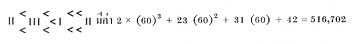
ข้อสังเกต
ตัวเลขบาบิโลน เป็นตัวเลขในระบบฐานหกสิบ เมื่อนำสัญลักษณ์ตัวเดิมไปวางไว้ในตำแหน่ง หรือหลักที่ต่างกัน จะได้ค่าต่างกัน เนื่องจากชาวบ้านบาบิโลนยังไม่รู้จักใช้สัญลักษณ์ศูนย์ จึงมีข้อยุ่งยากของการใช้ตัวเลขในระบบนี้ คือ ถ้าจำนวนในหลักใดขาดหายไป จะทำให้เกิดความสับสนในการอ่าน และ การเขียน
ตัวเลขกรีก
ในสมัยต้นๆ ชาวกรีกใช้สัญลักษณ์แทนจำนวนดังนี้

ในสมัยต่อมา กรีกเปลี่ยนมาใช้ตัวอักษร ซึ่งมียี่สิบเอ็ดตัว แทนจำนวนโดยใช้อักษรเก้าตัวแรกแทนหนึ่งถึงเก้า เก้าตัวถัดไป แทนสิบถึงเก้าสิบ และ เก้าตัวสุดท้ายแทนหนึ่งร้อยถึงเก้าร้อย ดังนี้

จำนวนที่ไม่ได้เขียนตัวอักษรกำกับไว้ หมายความว่า ตัวอักษรนั้นๆ เลิกใช้แล้ว

นอกจากจะใช้วิธีรวมค่าสัญลักษณ์แล้ว เมื่อต้องการเขียนสัญลักษณ์แทนจำนวนใหญ่ๆ ชาวกรีกจะใช้วิธีขีดเฉียง / เติมหน้าตัวอักษรนั้นๆ หมายถึง พันเท่าของจำนวนนั้นๆ

สัญลักษณ์ที่ใช้แทนจำนวนแบบนี้ ต้องอาศัยความจำมาก ไม่สะดวกในการเขียน อย่างไรก็ดี ความก้าวหน้าอย่างหนึ่งก็คือ การรู้จักคูณทวีพันเท่า
ตัวเลขโรมัน
ในสมัยต้นๆ ชาวโรมันใช้สัญลักษณ์เขียนแทนจำนวน ดังนี้



ตัวเลขโรมันที่ใช้ในปัจจุบัน แทนจำนวน
|
IV |
ห้าลบด้วยหนึ่ง |
สี่ |
|
VI |
ห้าบวกกับหนึ่ง |
หก |
|
IX |
สิบลบด้วยหนึ่ง |
เก้า |
|
XI |
สิบบวกกับหนึ่ง |
สิบเอ็ด |
|
XII |
สิบบวกกับสอง |
สิบสอง |
|
XIII |
สิบบวกกับสาม |
สิบสาม |
|
XIV |
สิบบวกกับสี่ |
สิบสี่ |
|
CMXIV |
พันลบด้วยร้อยบวกกับสิบสี่ |
เก้าร้อยสิบสี่ |
เป็นต้น
ตัวเลขจีน
ชาวจีนมีสัญลักษณ์สิบสองตัวที่ใช้เขียนแทนจำนวน

ชาวจีนใช้วิธีคูณตามค่าประจำตำแหน่งของแต่ละหลัก แล้วรวมผลคูณนั้นๆ เข้าด้วยกัน การเขียนเป็นดังนี้

ตัวเลขมายัน
ในสมัยก่อนที่โคลัมบัสพบซีกาโลกตะวันตกนั้น ชนเผ่ามายันได้อาศัยอยู่ในอเมริกากลาง และ เม็กซิโก เป็นชาติที่มีความเจริญรุ่งเรืองมาแล้ว ชาวมายันใช้ตัวเลขที่มีค่าประจำตำแหน่ง และ เป็นชาติแรกที่มีสัญลักษณ์แทนจำนวนศูนย์ สัญลักษณ์ที่ใช้แทนจำนวนของชาวมายัน มีดังนี้

การเขียนตัวเลขแทนจำนวนใหญ่ๆ ของชาวมายันใช้วิธีการเดียวกันกับของจีน คือเขียนในแนวตั้ง เรียงจากมากลงมาหาน้อย
เขียนตัวเลขหลักหน่วยไว้ตำแหน่งล่างสุด
เขียนตัวเลขหลักที่สองเหนือหลักหน่วย หลักที่สองมีค่าประจำตำแหน่งเป็น 20 เท่าของจำนวนในหลักนี้
เขียนตัวเลขหลักที่สามเหนือหลักที่สอง หลักที่สามมีค่าประจำตำแหน่งเป็น 18 X 20 เท่าของจำนวนในหลักนี้
เขียนตัวเลขหลักที่สี่ ที่ห้า ที่หก,... เหนือหลักที่ต่ำกว่าไปตามลำดับค่าประจำตำแหน่งจะเป็น 18 X 20^

