

 259,267 Views
259,267 Views
โดยทั่วไปเราคุ้นเคยกับหน่วยวัดมุมอย่าง "องศา" กันมาอยู่แล้ว หากเป็นรูปสามเหลี่ยมด้านเท่า ก็จะมีมุมภายในมุมละ 60 องศา มุมฉากเท่ากับ 90 องศา เส้นตรงมีมุม 180 องศา และวงกลมที่เราทราบกันดีว่ามีมุมภายในเท่ากับ 360 องศา แม้ว่าองศาจะไม่ใช่หน่วยในระบบหน่วยวัดสากล (SI) แต่ก็ได้รับการยอมรับให้ใช้กันอย่างกว้างขวาง
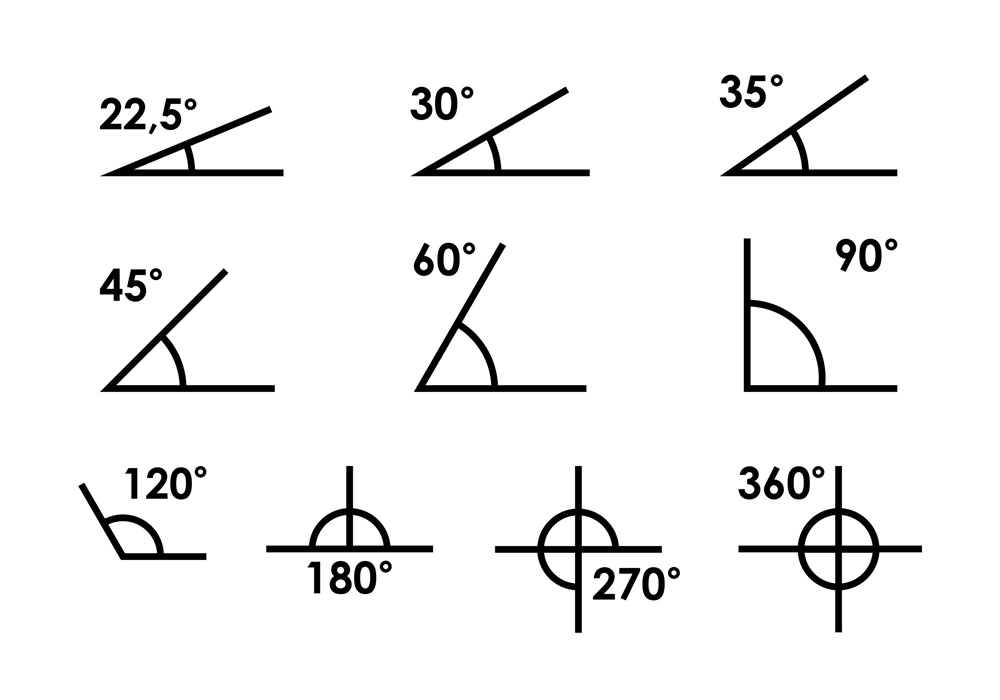
อย่างไรก็ตามนอกจากองศาแล้ว เรายังสามารถบอกขนาดของมุมในรูปแบบของ "เรเดียน (Radian)" ได้ด้วย และปัจจุบันเรเดียนนี้ก็เป็นหน่วยอนุพัทธ์ ในระบบเอสไอ โดยแทนด้วยสัญลักษณ์เฉพาะ "rad"
แม้ว่าเราจะใช้คำว่า "เรเดียน" ตามหลังตัวเลขบอกขนาดของมุม แต่แท้จริงแล้ว เรเดียนไม่ใช่หน่วย มันเป็นรูปแบบหนึ่งของการบอกขนาดมุมเท่านั้น เพียงแต่การเติมเรเดียนด้านหลังก็เพื่อให้เข้าใจตรงกันและใช้งานได้สะดวกขึ้น เรเดียนถูกใช้มานานแล้ว แต่กลับประกาศใช้และมีการให้คำจำกัดความประมาณปี 1870 โดยนักคณิตศาสตร์ โทมัส มูเยอร์ (Thomas Muir) และเจมส์ ทอมป์สัน (James Thompson) ซึ่งในเวลานั้นมีความลังเลระหว่างการใช้ rad, radial และ radian แต่ก็ปรับเปลี่ยนเป็นเรเดียนเมื่อปี 1874 และได้รับการตีพิมพ์เมื่อปี 1890 ในท้ายที่สุด
เรเดียนก็คือ อัตราส่วนระหว่าง ส่วนโค้งของวงกลมกับรัศมี หรือก็คือ θ = ส่วนโค้งของวงกลม/รัศมี หน่วยจึงหายไป ดังนั้น เรเดียนจึงไม่มีหน่วย หากสมมุติให้รัศมีวงกลมมีค่า 1 หน่วย ส่วนโค้งของวงกลมที่มีระยะจากรัศมีเส้นที่ 1 มายังรัศมีเส้นที่ 2 มีความยาว 1 หน่วยเท่ากับขนาดของรัศมี θ ก็จะมีค่าเท่ากับ 1 และเมื่อลองแบ่งวงกลมไปเรื่อย ๆ ทีละ θ = 1 จะได้มุมภายในวงกลมทั้งหมดเป็น θ = 6 และเหลือส่วนโค้งของวงกลมอีกเล็กน้อย
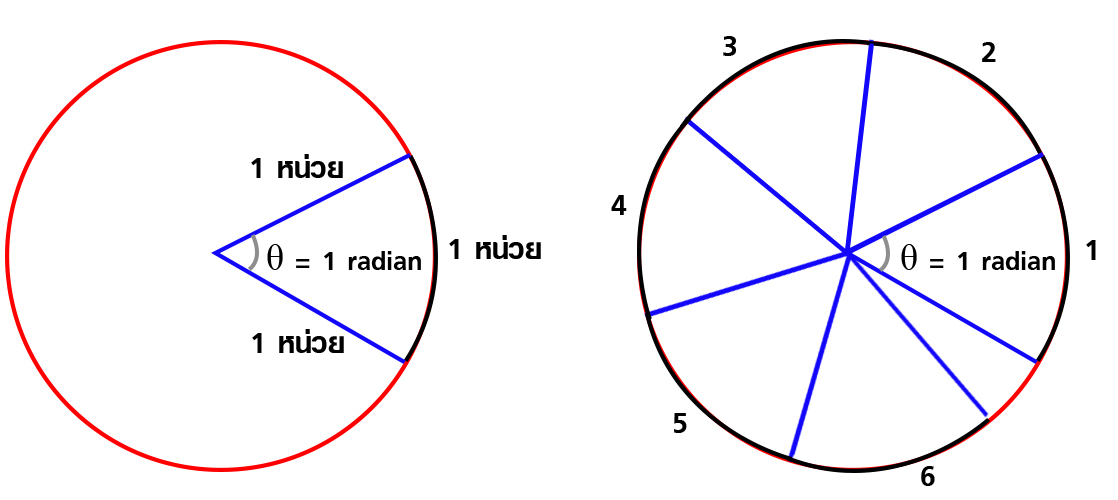
เราสามารถหาส่วนโค้งของวงกลมที่เหลืออยู่อีกเล็กน้อยได้จากสูตรเส้นรอบวง = 2πr และนิยาม θ = ส่วนโค้งของวงกลม/รัศมี
ซึ่งจะได้เป็น θ = 2πr/r
ดังนั้น θ = 2π
แต่ π = 3.14 หรือ 22/7 จึงได้เป็น θ = 2π = 2x3.14
ด้วยเหตุนี้ θ หรือมุมภายในวงกลมทั้งหมดจึงเท่ากับ 6.28 ซึ่งทำให้เราทราบว่า ส่วนโค้งของวงกลมที่เหลืออีกเล็กน้อยนั่นก็คือ 0.28
หากมุมภายในวงกลมทั้งหมดเป็น θ = 2π เมื่อเทียบกับหน่วยองศา จะเท่ากับ 360 องศา
ดังนั้น π = 180 องศา
หากต้องการทราบว่า 1 เรเดียนเป็นกี่องศา เราสามารถหาได้โดยการเทียบบัญญัติไตรยางค์
π เรเดียน เท่ากับ 180 องศา
ดังนั้น 1 เรเดียน เท่ากับ 180/π = 57.3 องศา
หากต้องการทราบว่า 1 องศาเป็นกี่เรเดียน เราสามารถหาได้โดยการเทียบบัญญัติไตรยางค์
180 องศา เท่ากับ π หรือ 3.14 เรเดียน
ดังนั้น 1 องศา เท่ากับ 3.14/180 = 0.0174 เรเดียน
หรือ ต้องการทราบว่า 120 องศา เป็นกี่เรเดียน เราสามารถหาได้โดยการเทียบบัญญัติไตรยางค์
180 องศา เท่ากับ π หรือ 3.14 เรเดียน
ดังนั้น 120 องศา เท่ากับ (πx120)/180 = 2π/3 หรือ 2.094 เรเดียน
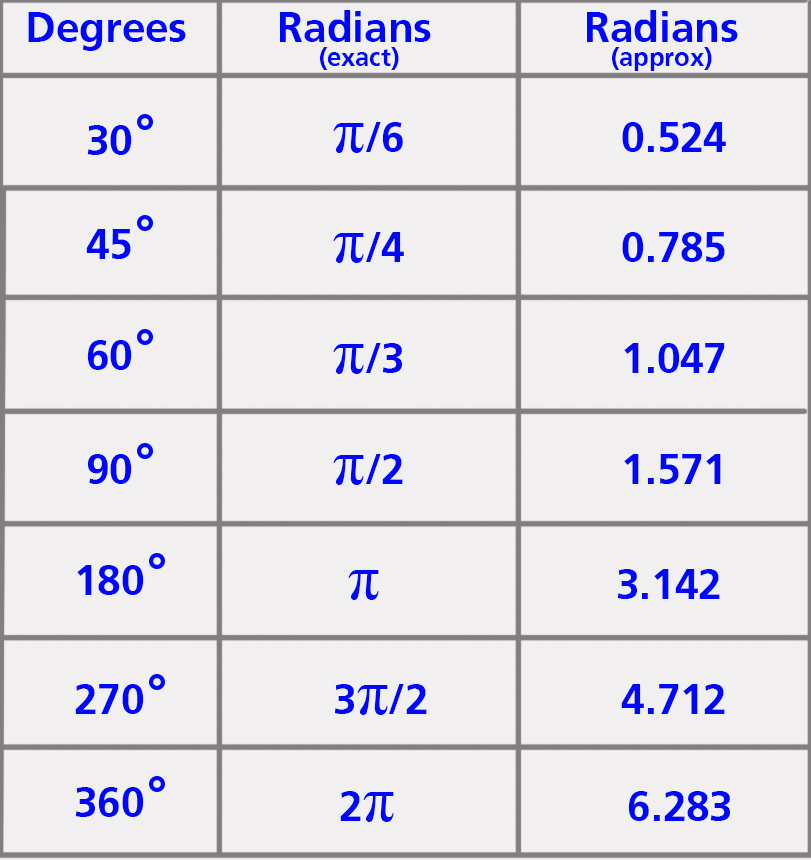
สำหรับค่าของเรเดียนที่องศาต่าง ๆ ที่ใช้บ่อย มีดังนี้
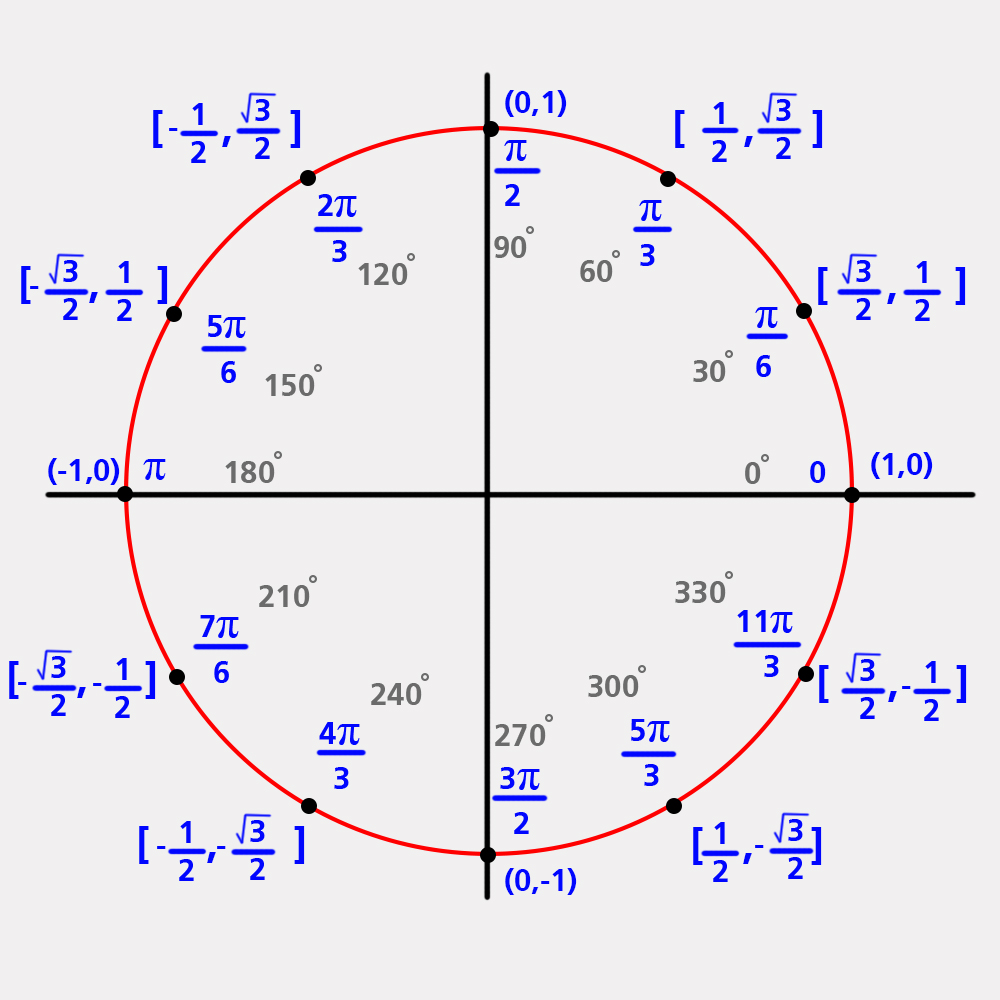
ส่วนใหญ่ในการศึกษาระดับชั้นสูง ๆ ตั้งแต่มัธยมศึกษาตอนปลายขึ้นไป จึงจะมีเรื่องของมุมเรเดียนเข้ามาเกี่ยวข้อง เนื่องจากเรเดียนเป็นหน่วยวัดมุมที่ใช้ในคณิตศาสตร์ขั้นสูง เช่น ตรีโกณมิติและแคลคูลัส หรือนำไปใช้ในการคำนวณทางฟิสิกส์ ซึ่งการคำนวณโดยใช้เรเดียนนี้จะเกี่ยวข้องกับตัวเลขน้อยกว่า ทำให้ความวุ่นวายหรือยุ่งยากในการคำนวณน้อยกว่า ตัวอย่างเช่น
สมการตรีโกณมิติในรูปแบบของเรเดียน
สมการตรีโกณมิติในรูปแบบขององศา
จะเห็นได้ว่าความวุ่นวายในสมการรูปแบบขององศานั้นมีมากกว่าเรเดียน และเหล่านี้เองที่ทำให้มุมเรเดียนยังคงถูกใช้อยู่อย่างกว้างขวางในวงการนักคณิตศาสตร์และวิทยาศาสตร์ รวมถึงวิชาชีพที่มีความเกี่ยวข้องกับการคำนวณเฉพาะทาง
บทความที่เกี่ยวข้อง
- ทำไมวงกลมมีมุมเท่ากับ 360 องศา
- ส่วนประกอบของวงกลม
