104,074 Views
104,074 Views
โดยทั่วไปการเคลื่อนที่ส่วนมากจะเป็นการเคลื่อนที่ที่ความเร็วไม่คงที่ เมื่อนำการเปลี่ยนแปลงความเร็วนั้นมาเทียบกับเวลา จึงได้ปริมาณการเปลี่ยนแปลงความเร็วเทียบกับเวลานั้น และนั่นคือ “ความเร่ง” หรือกล่าวได้ว่า ความเร่งก็คือ อัตราการเปลี่ยนแปลงความเร็วนั่นเอง โดยแทนด้วยสัญลักษณ์ a หน่วยของความเร่งมักใช้ m/s2 หรือเมตรต่อวินาที2 โดยการคำนวณอย่างง่ายเรามักจะประมาณให้ความเร่งมีค่าคงตัว จะสามารถหาความสัมพันธ์ต่าง ๆ ได้จากกราฟระหว่างความเร็วกับเวลา ดังนี้
สำหรับการเคลื่อนที่แนวตรง ความเร่งเป็นตัวแปรหนึ่งที่มีความสำคัญและเกี่ยวข้องกัน แต่นอกจากนี้ยังมีตัวแปรอื่น ๆ ที่เกี่ยวข้องกับการเคลื่อนที่แนวตรงด้วย เช่น
ความเร็วต้น หมายถึง ความเร็วเมื่อวัด ณ จุดเริ่มต้น มีสัญลักษณ์เป็น (u) มีหน่วยเป็น m/s หรือเมตรต่อวินาที
ความเร็วปลาย หมายถึง ความเร็วเมื่อวัด ณ จุดสิ้นสุด มีสัญลักษณ์เป็น (v) มีหน่วยเป็น m/s หรือเมตรต่อวินาที
เวลา มีสัญลักษณ์เป็น (t) มีหน่วยเป็น s หรือวินาที
ระยะกระจัด หมายถึง ระยะที่วัดจากจุดเริ่มต้นไปจนถึงจนสิ้นสุด มีสัญลักษณ์เป็น (s) มีหน่วยเป็น m หรือเมตร
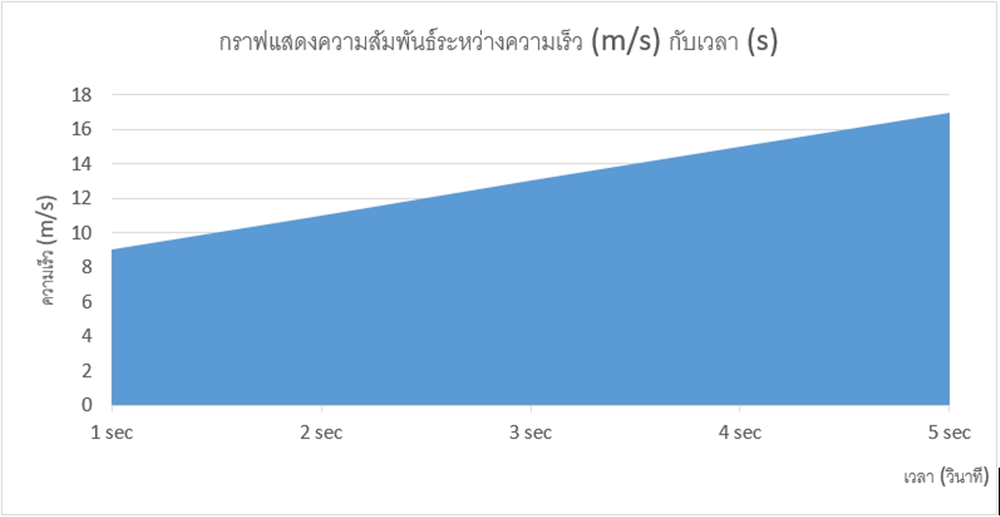
จากกราฟแสดงความสัมพันธ์ระหว่างความเร็ว (m/s) กับเวลา (s) ซึ่งเป็นกราฟเส้นตรง เราสามารถหาค่าความเร่งได้จากความชันของกราฟ คือ
เมื่อความชันกราฟหรือ Slope คือ ความเร่ง จะได้
โดย Δt หมายถึง การเปลี่ยนแปลงเวลา ซึ่ง Δt = t1 - t0 นั่นคือ
เมื่อให้ t0 คือ เวลาเริ่มต้น โดยส่วนมากมักจะมีค่าเป็น 0 และให้ t1 คือ เวลาตอนท้าย และกำหนดค่าเป็น t จะได้ว่า
จัดรูปสมการจะได้ หรือ
---------- (1)
นอกจากความชันของกราฟแสดงความสัมพันธ์ระหว่างความเร็ว (m/s) กับเวลา (s) จะมีความหมายดังกล่าวแล้ว พื้นที่ใต้กราฟยังหมายถึง ระยะกระจัด (s) ของการเคลื่อนที่ด้วย โดยจากกราฟแสดงความสัมพันธ์ระหว่างความเร็ว (m/s) กับเวลา (s) เราจะเห็นพื้นที่ใต้กราฟเป็นรูปสี่เหลี่ยมคางหมู และสามารถคำนวณหาพื้นที่ได้จากสมการ
พื้นที่มีค่าเท่ากับระยะกระจัด ความยาวของด้านคู่ขนานทั้งสองด้านมีค่าเป็นความเร็วต้นและความเร็วปลาย ส่วนระยะระหว่างด้านคู่ขนาน คือ เวลา
เมื่อแทนค่าจะได้ ---------- (2)
จากสมการ เมื่อจัดรูปแบบแล้วจะได้
นำสมการ แทนค่าลงใน
จะได้
นั่นคือ
จัดรูปสมการจะได้ ---------- (3)
และเมื่อแทนค่า สมการที่ (1) ลงไปในสมการที่ (2)
จะได้
เมื่อทำเป็นผลสำเร็จคือ ---------- (4)
สรุปได้ 4 สมการที่เกี่ยวข้องกับการเคลื่อนที่แนวตรงที่นิยมนำไปใช้คือ
---------- (1)
---------- (2)
---------- (3)
---------- (4)
ตัวอย่างความเร่งที่เห็นได้ในชีวิตประจำวันของเรานั่นคือ การขึ้นลิฟต์โดยสาร เนื่องจากความเร่งเป็นปริมาณเวกเตอร์ซึ่งมีทั้งขนาดและทิศทางจะส่งผลทำให้คนที่ใช้ลิฟต์โดยสารมักจะเกิดอาการต่าง ๆ ทำให้ยืนหรือทรงตัวได้ไม่ปกติ แบ่งได้ 2 ลักษณะคือ ขณะลิฟต์เคลื่อนขึ้น และขณะที่ลิฟต์เคลื่อนลง
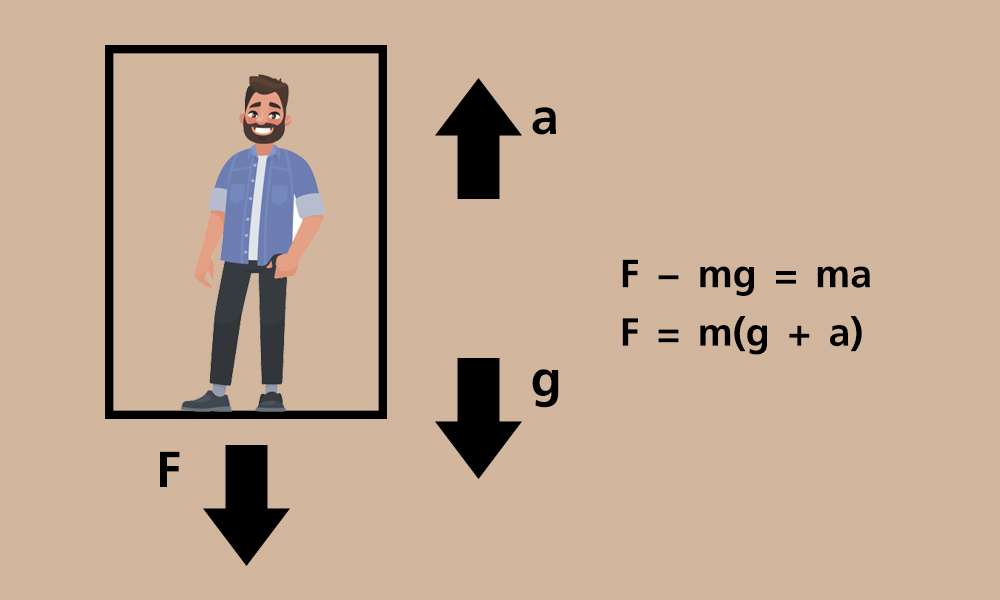
เมื่อลิฟต์เริ่มเคลื่อนที่ขึ้น ลิฟต์จะมีความเร่งในทิศชี้ขึ้น สวนทางกับความเร่งเนื่องจากแรงโน้มถ่วงของโลก จึงทำให้ผู้โดยสารภายในลิฟต์รู้สึกว่าตัวหนักขึ้น เพราะแรงที่ลิฟต์กระทำ ตามกฎข้อที่ 2 ของนิวตัน ดังสมการ ∑F = ma
เมื่อมีแรงที่กระทำ 2 แรงคือ แรงที่ลิฟต์ดึงขึ้น (F) และน้ำหนักของคน (mg)
แทนค่าจะได้ F – mg = ma
ดังนั้น F = m(g + a) จึงทำให้มีแรงมากขึ้นกว่าน้ำหนักเดิม
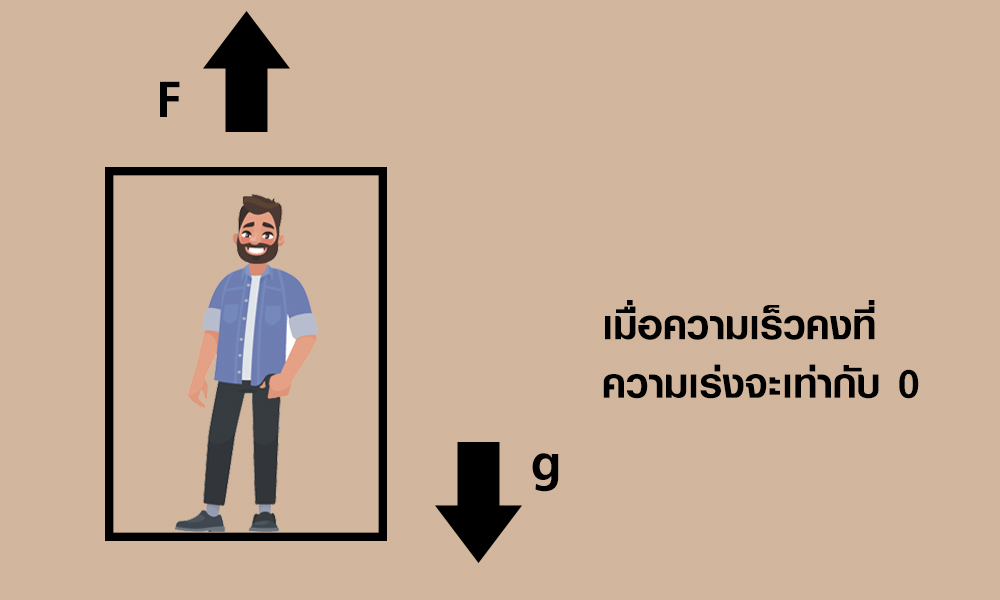
เมื่อลิฟต์เคลื่อนที่ขึ้นจนมีความเร็วคงที่ ลิฟต์จะมีความเร่งเป็น 0 ซึ่งทำให้ผู้โดยสารภายในลิฟต์รับแรงปกติเหมือนที่ยืนบนพื้นดิน ตามกฎข้อที่ 1 ของนิวตัน คือ ∑F = 0 จึงไม่รู้สึกถึงแรงกระทำ หรือความเร่งใด ๆ
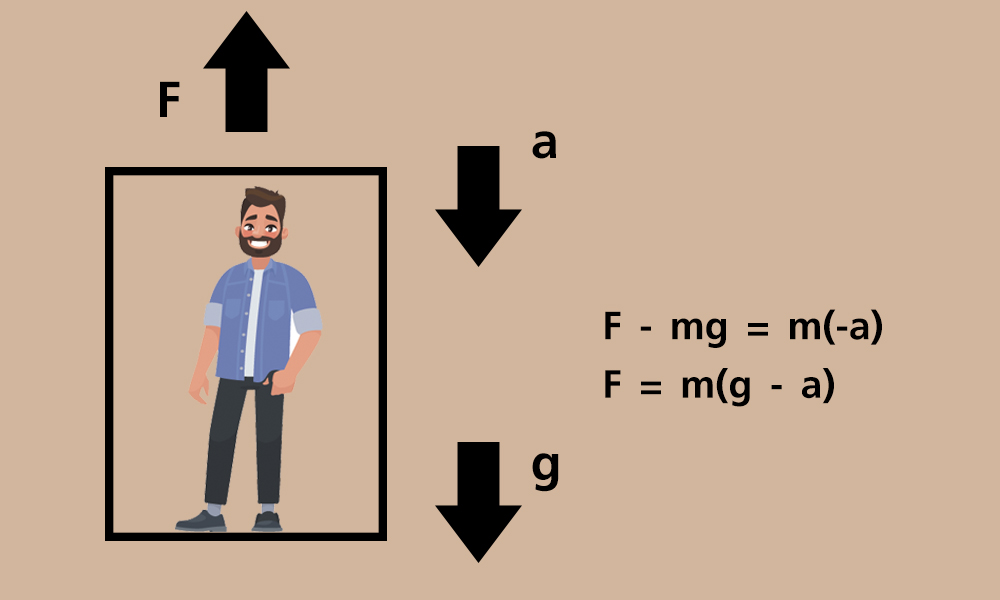
เมื่อลิฟต์เคลื่อนที่ขึ้นไปจนสุดและกำลังจะหยุด ลิฟต์จะมีความเร่งในทิศชี้ลง เป็นทิศเดียวกับความเร่งเนื่องจากแรงโน้มถ่วงของโลก จึงทำให้ผู้โดยสารรู้สึกว่าน้ำหนักตัวลดลง เพราะแรงที่ลิฟต์กระทำ ตามกฎข้อที่ 2 ของนิวตัน ดังสมการ ∑F = ma
แทนค่าจะได้ F – mg = m(-a)
ดังนั้น F = m(g - a) จึงทำให้มีแรงน้อยลงกว่าน้ำหนักเดิม
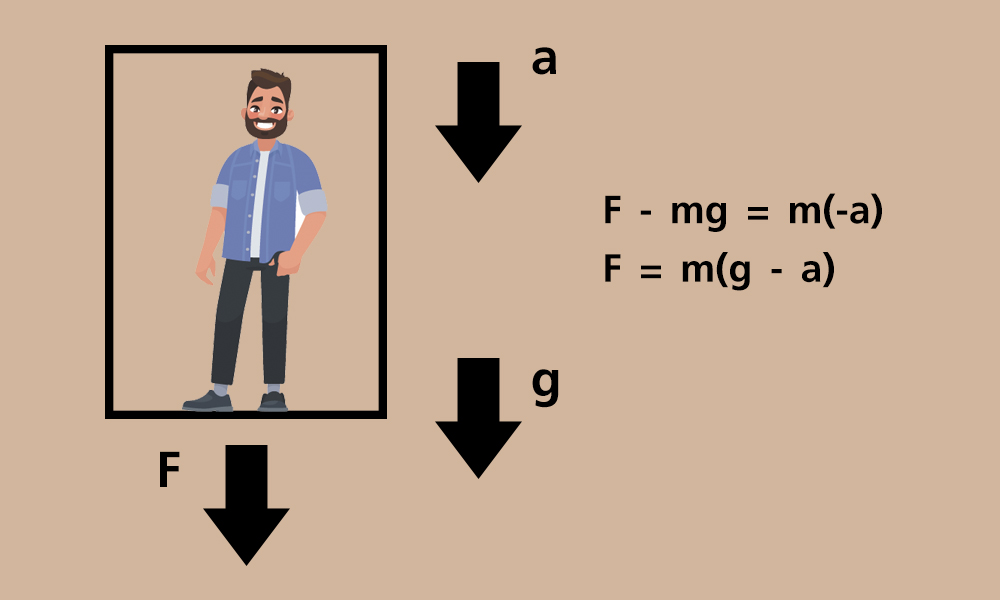
เมื่อลิฟต์เริ่มเคลื่อนที่ลง ลิฟต์จะมีความเร่งในทิศชี้ลง ทิศเดียวกับความเร่งเนื่องจากแรงโน้มถ่วงของโลก จึงทำให้ผู้โดยสารภายในลิฟต์รู้สึกว่าตัวเบาลง เพราะแรงที่ลิฟต์กระทำ ตามกฎข้อที่ 2 ของนิวตัน ดังสมการ ∑F = ma
เมื่อมีแรงที่กระทำ 2 แรงคือ แรงที่ลิฟต์ดึงลง (F) และน้ำหนักของคน (mg)
แทนค่าจะได้ F – mg = m(-a)
ดังนั้น F = m(g - a) จึงทำให้มีแรงน้อยลงกว่าน้ำหนักเดิม
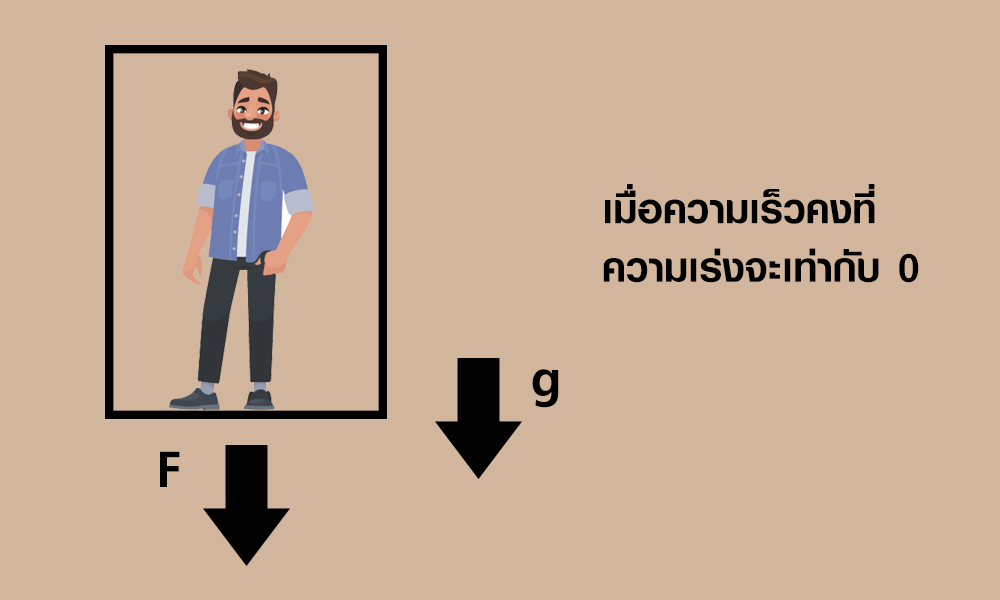
เมื่อลิฟต์เคลื่อนที่ลงจนมีความเร็วคงที่ ลิฟต์จะมีความเร่งเป็น 0 ซึ่งทำให้ผู้โดยสารภายในลิฟต์รับแรงปกติเหมือนที่ยืนบนพื้นดิน ตามกฎข้อที่ 1 ของนิวตัน จึงไม่รู้สึกถึงแรงกระทำ หรือความเร่งใด ๆ
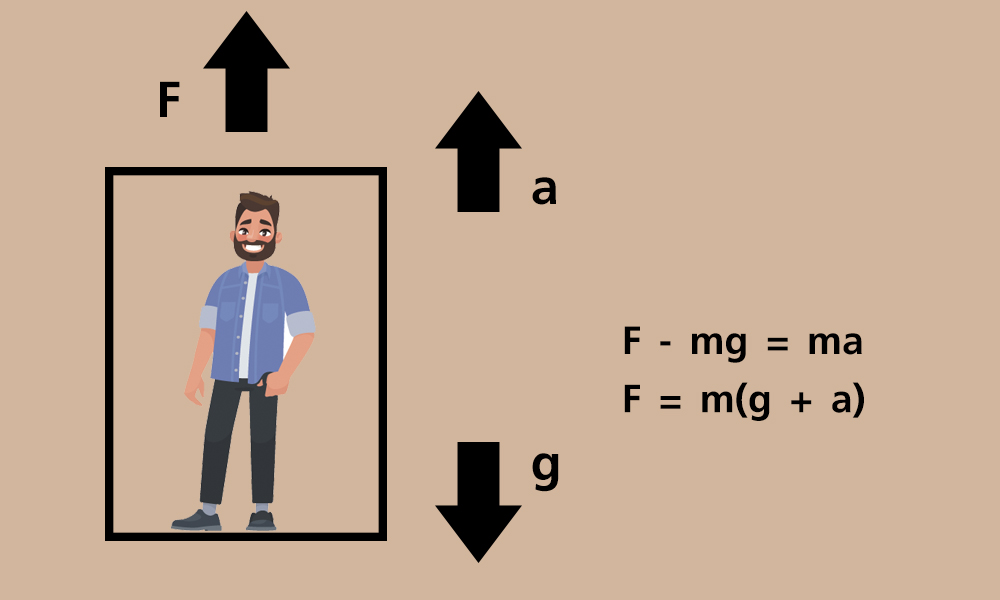
เมื่อลิฟต์เคลื่อนที่ลงและกำลังจะหยุด ลิฟต์จะมีความเร่งในทิศชี้ขึ้น สวนทางกับความเร่งเนื่องจากแรงโน้มถ่วงของโลก จึงทำให้ผู้โดยสารภายในลิฟต์รู้สึกว่าตัวหนักขึ้น เพราะแรงที่ลิฟต์กระทำ ตามกฎข้อที่ 2 ของนิวตัน ดังสมการ ∑F = ma
เมื่อมีแรงที่กระทำ 2 แรงคือ แรงที่ลิฟต์ดึงขึ้น (F) และน้ำหนักของคน (mg)
แทนค่าจะได้ F – mg = ma
ดังนั้น F = m(g + a) จึงทำให้มีแรงมากขึ้นกว่าน้ำหนักเดิม