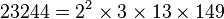จำนวนเฉพาะ
ทีมงานทรูปลูกปัญญา | 2010-10-23 13:31:51
ในคณิตศาสตร์ จำนวนเฉพาะ คือ จำนวนธรรมชาติที่มีตัวหารที่เป็นบวกอยู่ 2 ตัว คือ 1 กับตัวมันเอง ตรงข้ามกับจำนวนประกอบ
ลำดับของจำนวนเฉพาะเริ่มต้นด้วย
สำหรับจำนวนเฉพาะ 500 จำนวนแรก สำหรับเลข 1 ไม่ถือว่าเป็นจำนวนเฉพาะตามนิยาม
เซตของจำนวนเฉพาะทั้งหมดมักเขียนแทนด้วย  เนื่องจาก 2 เป็นจำนวนเฉพาะตัวเดียวที่เป็นเลขคู่ ดังนั้นคำว่า จำนวนเฉพาะคี่ จะถูกใช้เพื่อหมายถึงจำนวนเฉพาะทั้งหมดที่ไม่ใช่ 2
เนื่องจาก 2 เป็นจำนวนเฉพาะตัวเดียวที่เป็นเลขคู่ ดังนั้นคำว่า จำนวนเฉพาะคี่ จะถูกใช้เพื่อหมายถึงจำนวนเฉพาะทั้งหมดที่ไม่ใช่ 2
การแทนจำนวนธรรมชาติ ด้วยผลคูณของจำนวนเฉพาะ
ทฤษฎีบทมูลฐานของเลขคณิตกล่าวว่า จำนวนเต็มบวกทุกตัวสามาถเขียนได้ในรูปผลคูณของจำนวนเฉพาะ และเขียนได้แบบเดียวเท่านั้น จำนวนเฉพาะเป็นเหมือน "บล็อกก่อสร้าง"ของจำนวนธรรมชาติ ตัวอย่างเช่น
ไม่ว่าเราจะแยกตัวประกอบของ 23244 แบบใดโดยไม่คำนึงถึงลำดับของตัวประกอบแล้ว มันก็จะไม่ต่างไปจากนี้
มีจำนวนเฉพาะอยู่จำนวนเท่าไร?
มีจำนวนเฉพาะอยู่เป็นจำนวนมากโดยหาค่ามิได้ บทพิสูจน์ที่เก่าแก่ที่สุดสำหรับประโยคนี้ คิดขึ้นโดยนักคณิตศาสตร์ชาวกรีกชื่อ ยุคลิด ในหนังสือ Elements (Book IX, Proposition 20) ยุคลิดกล่าวในหนังสือของเขาว่า "มีจำนวนเฉพาะ มากกว่าจำนวนเฉพาะ[จำนวนจำกัด]ที่กำหนดให้" บทพิสูจน์ของเขาสามารถสรุปย่อๆได้ว่า:
- ให้ดูจำนวนเฉพาะมีจำนวนจำกัด ซึ่งเรากำหนดว่ามันเป็นจำนวนเฉพาะที่มีอยู่ทั้งหมด คูณจำนวนทั้งหมดเข้าด้วยกันและ บวก 1 ผลลัพธ์ที่ได้จะไม่สามารถหารด้วยจำนวนเฉพาะใดๆใสสนเซตได้ เพราะว่าไม่ว่าจะหารด้วยตัวใดก็จะเหลือเศษ 1 ดังนั้น มันจะต้องเป็นจำนวนเฉพาะ หรืออาจจะมีจำนวนเฉพาะที่หารมันลงตัวแต่ไม่ได้อยู่ในเซตจำกัดนี้ ดังนั้น เซตนี้ไม่ได้มีจำนวนเฉพาะทั้งหมด
- การค้นหาจำนวนเฉพาะ
ตะแกรงเอราทอสเทนีส และ ตะแกรงของ Atkin เป็นวิธีที่ใช้สร้างรายการจำนวนเฉพาะทั้งหมดตามจำนวนที่กำหนดอย่างรวดเร็ว
ในทางปฏิบัติ เราต้องการตรวจสอบว่าเลขที่กำหนดให้ว่าเป็นจำนวนเฉพาะหรือไม่ มากกว่าจะสร้างรายการจำนวนเฉพาะทั้งหมดขึ้นมา ซึ่งวิธีที่ทดสอบ จะให้คำตอบด้วยความน่าจะเป็น เราสามารถตรวจสอบเลขที่มีขนาดใหญ่ (มี 1 พันหลักขึ้นไป) ว่าเป็นจำนวนเฉพาะหรือไม่ได้อย่างรวดเร็ว โดยใช้การทดสอบความเป็นจำนวนเฉพาะด้วยความน่าจะเป็น (probabilistic primality tests) ซึ่งวิธีนี้ จะต้องทำการสุ่มตัวเลขขึ้นมาตัวหนึ่ง เรียกว่า "พยาน" (witness) และใช้สูตรที่เกี่ยวข้องกับพยาน และจำนวนเฉพาะ N ทำการทดสอบ หลังจากที่ทดสอบไปหลายรอบ เราจะตอบได้ว่า N เป็น"จำนวนประกอบอย่างแน่นอน" หรือ N "อาจเป็นจำนวนเฉพาะ" วิธีทดสอบไม่สามารถให้คำตอบได้ว่าเป็นจำนวนเฉพาะอย่างแน่นอนหรือไม่ การทดสอบบางครั้ง เมื่อใส่จำนวนประกอบลงไป ก็ให้คำตอบว่า"อาจเป็นจำนวนเฉพาะ"เสมอ ไม่ว่าจะเลือกพยานตัวใดก็ตาม จำนวนเหล่านี้เรียกว่า จำนวนเฉพาะเทียม (pseudoprimes) สำหรับการทดสอบ
-
สมบัติบางประการของจำนวนเฉพาะ
- ถ้า p เป็นจำนวนเฉพาะ และ p หาร ab ลงตัวแล้ว p หาร a ลงตัว หรือ p หาร b ลงตัว ประพจน์นี้พิสูจน์โดยยุคลิด และมีชื่อเรียกว่า บทตั้งของยุคลิด ใช้ในการพิสูจน์เรื่องการแยกตัวประกอบได้อย่างเดียว
- ริง (ดูที่เลขคณิตมอดุลาร์) Z/nZ เป็นฟีลด์ ก็ต่อเมื่อ n เป็นจำนวนเฉพาะ
- ถ้า p เป็นจำนวนเฉพาะ และ a เป็นจำนวนเต็มใดๆแล้ว ap − a หารด้วย p ลงตัว (ทฤษฎีบทน้อยของแฟร์มาต์)
- จำนวนเต็ม p > 1 เป็นจำนวนเฉพาะ ก็ต่อเมื่อ (p − 1) ! 1 หารด้วย p ลงตัว (ทฤษฎีบทของวิลสัน). บทกลับ, จำนวนเต็ม n > 4 เป็นจำนวนประกอบ ก็ต่อเมื่อ (n − 1) ! หารด้วย n ลงตัว
- ถ้า n เป็นจำนวนเต็มบวกแล้ว จะมีจำนวนเฉพาะ p ที่ n < p < 2n (สัจพจน์ของเบอร์แทรนด์)
- สำหรับจำนวนเฉพาะ p > 2 จะมีจำนวนธรรมชาติ n ที่ทำให้ p = 4n ± 1
- สำหรับจำนวนเฉพาะ p > 3 จะมีจำนวนธรรมชาติ n ที่ทำให้ p = 6n ± 1
การประยุกต์
จำนวนเฉพาะที่มีขนาดใหญ่มาก (ใหญ่กว่า 10100) นำไปใช้ประโยชน์ในอัลกอริทึมเข้ารหัสลับแบบกุญแจสาธารณะ นอกจากนี้ยังใช้ในตารางแฮช (hash tables) และเครื่องสุ่มเลขเทียม
- ช่องว่างระหว่างจำนวนเฉพาะ
ให้ pn คือจำนวนเฉพาะตัวที่ n (นั่นคือ p1 = 2, p2 = 3, ...) ช่องว่าง gn ระหว่างจำนวนเฉพาะ pn กับ pn 1 คือผลต่างของจำนวนเฉพาะสองจำนวนดังกล่าว นั่นคือ
-
- gn = pn 1 − pn
เราจะได้ g1 = 3 − 2 = 1, g2 = 5 − 3 = 2, g3 = 7 − 5 = 2, และ g4 = 11 − 7 = 4 ลำดับ gn ของช่องว่างระหว่างจำนวนเฉพาะ เป็นลำดับที่มีการศึกษากันอย่างมาก
สำหรับจำนวนนับ N ใดๆ ที่มากกว่า 1
-
- N! 2, N! 3, ..., N! N
เป็นลำดับของจำนวนประกอบที่ติดกัน N − 1 ตัว ดังนั้น เราสามารถสร้างช่องว่างระหว่างจำนวนเฉพาะให้มีขนาดใหญ่เท่าใดก็ได้ นั่นคือ สำหรับจำนวน N ใดๆ จะมีจำนวนเต็ม n ซึ่ง gn > N (เลือก n ที่ทำให้ pn มีค่ามากที่สุด และน้อยกว่า N! 2)
ช่องว่างระหว่างจำนวนเฉพาะใดๆ มีค่าน้อยมากเมื่อเทียบกับจำนวนเฉพาะ ดังนั้น gn/pn จึงมีค่าเข้าใกล้ 0 เมื่อ n เข้าใกล้อนันต์ ข้อความคาดการณ์จำนวนเฉพาะคู่แฝดกล่าวว่า มี n ที่ทำให้ gn = 2 อยู่ไม่จำกัด
-
-
จำนวนเฉพาะที่มากที่สุดเท่าที่รู้
จำนวนเฉพาะที่มากที่สุดเท่าที่รู้ตั้งแต่ ธันวาคม พ.ศ. 2549 คือ 230402457 − 1 (ตัวเลขนี้มีความยาว 9,152,052 หลัก) มันเป็นจำนวนเฉพาะแมร์กแซนตัวที่ 43 M30402457 ถูกค้นพบเมื่อวันที่ 15 ธันวาคม พ.ศ. 2549 โดยดร.สตีเฟน บูนและ ดร.เคอร์ติส คูเปอร์ สมาชิกของ GIMPS
จำนวนเฉพาะที่มากที่สุดเท่าที่รู้รองลงมากันยายน พ.ศ. 2548 คือ 225964951 − 1 (ตัวเลขนี้มีความยาว 7,816,230 หลัก) มันเป็นจำนวนเฉพาะแมร์กแซนตัวที่ 42 M25964951 ถูกค้นพบเมื่อวันที่ 18 กุมภาพันธ์ พ.ศ. 2548 โดยMartin Nowak สมาชิกที่มีบทบาทของ GIMPS
จำนวนเฉพาะที่มากที่สุดเท่าที่รู้รองลงมา คือ 224036583 − 1 (ตัวเลขนี้มีความยาว 7,235,733 หลัก) มันเป็นจำนวนเฉพาะแมร์กแซนตัวที่ 41 M24036583 ถูกค้นพบเมื่อวันที่ 15 พฤษภาคม พ.ศ. 2547 โดยJosh Findley (สมาชิกของ GIMPS) และประกาศในปลายเดือนพฤษภาคม พ.ศ. 2547
จำนวนเฉพาะที่มากเป็นอันดับสามเท่าที่รู้ คือ 220996011 − 1 (ตัวเลขนี้มีความยาว 6,320,430 หลัก) มันเป็นจำนวนเฉพาะแมร์กแซนตัวที่ 40 M20996011 ถูกค้นพบเมื่อวันที่ 17 พฤศจิกายน พ.ศ. 2546 โดยMichael Shafer (และ GIMPS) และประกาศในต้นเดือนธันวาคม พ.ศ. 2546
-
-
แหล่งที่มาของข้อมูล https://th.wikipedia.org/wiki/%E0%B8%88%E0%B8%B3%E0%B8%99%E0%B8%A7%E0%B8%99%E0%B9%80%E0%B8%89%E0%B8%9E%E0%B8%B2%E0%B8%B0