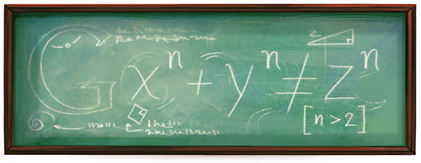
ก่อนอื่น ต้องรู้ ประวัติก่อน
ปีแยร์ เดอ แฟร์มา (ฝรั่งเศส: Pierre de Fermat; 17 สิงหาคม 1601 หรือ 1607/8 – 12 มกราคม 1665) เป็นชาวฝรั่งเศส ผู้เป็นนักกฎหมายประจำสภานิติบัญญัติประจำแคว้นตูลูซ และเป็นนักคณิตศาสตร์มือสมัครเล่นที่ได้ชื่อเสียงมาจากริเริ่มพัฒนาการหลายแขนงอันนำไปสู่แคลคูลัสกณิกนันต์ (infinitesimal calculus) รวมถึง การกะความเท่าเทียม (adequality) โดยเฉพาะอย่างยิ่ง เป็นที่นิยมกันว่า เขาค้นพบวิธีดั้งเดิมสำหรับคำนวณเส้นโค้งที่กว้างที่สุดและที่เล็กที่สุด อันเทียบได้กับ เส้นโค้งลักษณะเฉพาะ(characteristic curv) ใน สมการเชิงอนุพันธ์ (differential equation) ในวิชาการปัจจุบัน นอกจากนี้ เขายังเป็นที่ร่ำลือในเรื่องงานค้นคว้าเกี่ยวกับทฤษฎีตัวเลข (number theory) ด้วย

ทฤษฎีบทสุดท้ายของแฟร์มาต์ (อังกฤษ: Fermat's last theorem) เป็นหนึ่งในทฤษฎีบทที่โด่งดังในประวัติศาสตร์ของคณิตศาสตร์ ซึ่งกล่าวว่า:
|
ปิแยร์ เดอ แฟร์มาต์ นักคณิตศาสตร์ในคริสต์ศตวรรษที่ 17 ได้เขียนทฤษฎีบทนี้ลงในหน้ากระดาษหนังสือ Arithmetica ของไดโอแฟนตัส ฉบับแปลเป็นภาษาละตินโดย Claude-Gaspar Bachet เขาเขียนว่า "ฉันมีบทพิสูจน์ที่น่าอัศจรรย์สำหรับบทสรุปนี้ แต่พื้นที่กระดาษเหลือน้อยเกินไปที่จะอธิบายได้" (เขียนเป็นภาษาละตินว่า "Cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet.") อย่างไรก็ตาม ตลอดระยะเวลา 357 ปี ไม่มีใครสามารถพิสูจน์ได้ถูกต้องเลย
ข้อความนี้มีความสำคัญมาก เพราะว่าข้อความอื่นๆ ที่แฟร์มาต์เขียนนั้น ได้รับการพิสูจน์หมดแล้ว ไม่ว่าจะพิสูจน์ด้วยตัวเขาเอง หรือว่ามีคนให้บทพิสูจน์ในภายหลัง ทฤษฎีบทนี้ไม่ได้เป็นข้อความคาดการณ์สุดท้ายที่แฟร์มาต์เขียน แต่เป็น ข้อสุดท้ายที่จะต้องพิสูจน์ นักคณิตศาสตร์ได้พยายามพิสูจน์หรือไม่ก็หักล้างทฤษฎีบทนี้มาโดยตลอด และต้องพบกับความล้มเหลวทุกครั้งไป ทำให้ทฤษฎีนี้เป็นทฤษฎีที่สร้างบทพิสูจน์ที่ผิดๆ มากที่สุดในวงการคณิตศาสตร์ก็ว่าได้ อาจเป็นเพราะทฤษฎีบทนี้ดูแล้วไม่มีอะไรซับซ้อนนั่นเอง

บริบททางคณิตศาสตร์
ทฤษฎีบทสุดท้ายของแฟร์มาต์ เป็นรูปแบบทั่วไปของสมการไดโอแฟนไทน์ a2 b2 = c2 (สมการที่ตัวแปรเป็นจำนวนเต็มเท่านั้น) ชาวจีน ชาวกรีก และชาวบาบิโลเนียนได้ค้นพบคำตอบของสมการนี้หลายคำตอบเช่น (3, 4, 5) (32 42 = 52) หรือ (5, 12, 13) เป็นต้น คำตอบเหล่านี้เรียกว่า สามสิ่งอันดับพีทาโกรัส (Pythagorean triples) และมีอยู่จำนวนไม่จำกัด ทฤษฎีบทสุดท้ายของแฟร์มาต์ กล่าวว่า สมการนี้จะไม่มีคำตอบเมื่อเลขยกกำลังมากกว่า 2
ทฤษฎีนี้ไม่ค่อยถูกนำไปใช้ประโยชน์มากนัก (ไม่ได้ถูกนำไปใช้พิสูจน์ทฤษฎีอื่น) แต่มันก็เชื่อมโยงกับคณิตศาสตร์สาขาอื่น ๆ หลายสาขา และมันก็ไม่เป็นความพยายามที่ไร้สาระเสียทีเดียว การพยายามพิสูจน์ทฤษฎีนี้ก่อให้เกิดคณิตศาสตร์สาขาต่าง ๆ ที่สำคัญอีกมากมาย
บทพิสูจน์
แอนดรูว์ ไวลส์ (Andrew Wiles) นักคณิตศาสตร์ชาวอังกฤษจากมหาวิทยาลัยแคมบริดจ์ ได้พิสูจน์ทฤษฎีบทสุดท้ายของแฟร์มาต์ โดยใช้เครื่องมือในการพิสูจน์คือ เรขาคณิตเชิงพีชคณิต (ในเรื่องเส้นโค้งเชิงวงรี และรูปแบบมอดุลาร์) , ทฤษฎีกาโลอิส และ พีชคณิต Hecke โดยได้รับความช่วยเหลือจาก ริชาร์ด เทย์เลอร์ (Richard Taylor) ซึ่งเป็นลูกศิษย์ของเขาเอง บทพิสูจน์ของเขาได้ตีพิมพ์ลงในวารสาร Annals of Mathematics เมื่อค.ศ. 1995
ไวลส์ใช้เวลา 7 ปีในการพิสูจน์ทฤษฎีบทสุดท้ายของแฟร์มาต์ เขาทำการพิสูจน์โดยลำพัง และเก็บเรื่องนี้เป็นความลับมาโดยตลอด (ยกเว้น ตอนตรวจทานครั้งสุดท้าย ซึ่งเขาได้ขอความช่วยเหลือจากเพื่อนของเขาที่ชื่อNick Katz) ในวันที่ 21-23 มิถุนายน ค.ศ. 1993 เขาก็ได้แสดงบทพิสูจน์ของเขาที่มหาวิทยาลัยเคมบริดจ์ ผู้เข้าฟังการบรรยายครั้งนั้นต่างก็ประหลาดใจไปกับวิธีการต่างๆ ในบทพิสูจน์ของเขา ต่อมา เขาก็พบข้อผิดพลาดในบทพิสูจน์ แต่ไวลส์และเทย์เลอร์ยังไม่ละทิ้งความพยายาม เขาใช้เวลาอยู่หนึ่งปีในการแก้ไข และในเดือนกันยายน ค.ศ. 1994 เขาก็ได้เสนอบทพิสูจน์ใหม่อีกครั้งโดยใช้วิธีการที่แตกต่างไปจากเดิม เรื่องการพิสูจน์นี้จึงเป็นเรื่องที่น่าจดจำเลยทีเดียว
นี่คือข้อความที่แฟร์มาต์เขียนไว้บนหน้ากระดาษหนังสือ Arithmetica:
Cubum autem in duos cubos, aut quadrato-quadratum in duos quadrato-quadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duos eiusdem nominis fas est dividere cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exigitas non caperet.
(มันเป็นไปไม่ได้ที่จะแบ่งจำนวนยกกำลัง 3 ออกเป็นจำนวนยกกำลัง 3 สองจำนวน หรือแบ่งจำนวนยกกำลัง 4 ออกเป็นจำนวนยกกำลัง 4 สองจำนวน หรือกล่าวโดยทั่วไปว่า ไม่สามารถแบ่งจำนวนที่ยกกำลังมากกว่า 2 ออกเป็นจำนวนที่ยกกำลังเท่าเดิมสองจำนวนได้ ฉันมีบทพิสูจน์ที่น่าอัศจรรย์สำหรับบทสรุปนี้ แต่ขอบกระดาษนี้มีพื้นที่น้อยเกินกว่าที่จะเขียนบรรยายได้)
หลายคนต่างสงสัยใน "บทพิสูจน์ที่น่าอัศจรรย์" ของแฟร์มาต์ว่ามันมีอยู่จริงหรือไม่ บทพิสูจน์ของไวลส์นั้น หนาประมาณ 200 หน้า และยากเกินกว่าที่นักคณิตศาสตร์ในปัจจุบันจะเข้าใจ ในขณะที่บทพิสูจน์ของแฟร์มาต์น่าจะใช้วิธีที่พื้นฐานมากกว่านี้ เนื่องจากข้อจำกัดด้านความรู้ทางด้านคณิตศาสตร์ในสมัยนั้น ซึ่งก็เป็นเหตุให้นักคณิตศาสตร์และนักประวัติศาสตร์ที่เชี่ยวชาญด้านวิทยาศาสตร์ส่วนใหญ่ก็ยังไม่ค่อยเชื่อว่าแฟร์มาต์จะมีบทพิสูจน์ที่ถูกต้องสำหรับเลขยกกำลัง n ทุกจำนวนจริงๆ
แอนดรูส์ ไวลส์ เองก็เคยให้สัมภาษณ์ไว้ว่าเขาไม่เชื่อว่าแฟร์มาต์จะมีบทพิสูจน์ที่ถูกต้องจริง
I don’t believe Fermat had a proof. I think he fooled himself into thinking he had a proof. But what has made this problem special for amateurs is that there’s a tiny possibility that there does exist an elegant seventeenth century proof.
(ผมไม่เชื่อว่าแฟร์มาต์จะมีบทพิสูจน์ที่ถูกต้องจริง ผมคิดว่าเขาหลอกให้ตัวเองเชื่อว่าเขามีบทพิสูจน์นั้น แต่สิ่งที่ทำให้โจทย์ข้อนี้เป็นเรื่องพิเศษสำหรับนักคณิตศาสตร์สมัครเล่นก็คือ มันทำให้เกิดความหวังว่า ยังมีโอกาสที่จะค้นพบบทพิสูจน์อันสวยงามได้โดยใช้เพียงความรู้คณิตศาสตร์ในศตวรรษที่ 17)
อย่างไรก็ตามความผิดพลาดเป็นเรื่องธรรมดาของมนุษย์ ดังเคยมีตัวอย่างมากมายของนักคณิตศาสตร์หรือนักวิทยาศาสตร์ชื่อดังที่ได้มีความเชื่อที่ผิดพลาดหลายท่าน ดังเช่นไอน์สไตน์ครั้งหนึ่งก็ยังให้ข้อสรุปที่ผิดพลาดเกี่ยวกับการขยายตัวของจักรวาล เพราะฉะนั้นจึงไม่น่าจะแปลกใจอะไรถ้าแฟร์มาต์จะเข้าใจผิดว่าเขามีบทพิสูจน์ที่ถูกต้องจริง.
แหล่งที่มาของข้อมูล https://th.wikipedia.org/wiki/ทฤษฎีบทสุดท้ายของแฟร์มา

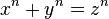 เมื่อ n เป็นจำนวนเต็มที่มากกว่า 2
เมื่อ n เป็นจำนวนเต็มที่มากกว่า 2