พาย หรือ ไพ (pi: π) เป็นค่าคงตัวทางคณิตศาสตร์ ที่เกิดจากความยาวเส้นรอบวงหารด้วยเส้นผ่านศูนย์กลางของวงกลม ค่า π มักใช้ในคณิตศาสตร์, ฟิสิกส์ และวิศวกรรม π เป็นอักษรกรีกที่ตรงกับตัว "p" ในอักษรละติน มีชื่อว่า "pi" (อ่านว่า พาย ในภาษาอังกฤษ แต่อ่านว่า พี ในภาษากรีก) บางครั้งเรียกว่า ค่าคงตัวของอาร์คิมิดีส หรือจำนวนของลูดอฟ
ในเรขาคณิตแบบยุคลิด π มีนิยามว่าเป็นอัตราส่วนของเส้นรอบวงหารด้วยเส้นผ่านศูนย์กลางของวงกลม หรือเป็นอัตราส่วนของพื้นที่วงกลม หารด้วย รัศมียกกำลังกำลังสอง ในคณิตศาสตร์ชั้นสูงจะนิยาม π โดยใช้ฟังก์ชันตรีโกณมิติ เช่น π คือจำนวนบวก x ที่น้อยสุดที่ทำให้ sin(x) = 0
ค่า π โดยประมาณ 50 ตำแหน่งคือ
- 3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510
แม้ว่าค่านี้มีความละเอียดพอที่จะใช้ในงานวิศวกรรมหรือวิทยาศาสตร์แล้ว ปัจจุบันมีการคำนวณค่า π ได้หลายตำแหน่ง ซึ่งหาได้ทั่วไปจากอินเทอร์เน็ต คอมพิวเตอร์ส่วนบุคคลโดยทั่วไปสามารถคำนวณค่า π ได้พันล้านหลัก ขณะที่ซูเปอร์คอมพิวเตอร์คำนวณค่า π ได้เกินล้านล้านหลัก และไม่พบว่ามีรูปแบบที่ซ้ำกันของค่า π ปรากฏอยู่
สูตรที่เกี่ยวข้องกับ π
เรขาคณิต
π มักปรากฏในสูตรที่เกี่ยวกับวงกลมและทรงกลม
| รูปร่างทางเรขาคณิต | สูตร |
|---|---|
| เส้นรอบวงของวงกลมที่มีรัศมี r และเส้นผ่านศูนย์กลาง d |  |
| พื้นที่ของวงกลมที่มีรัศมี r |  |
| พื้นที่ของวงรีที่มีแกนเอก a และแกนโท b | 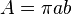 |
| ปริมาตรของทรงกลมที่มีรัศมี r และเส้นผ่านศูนย์กลาง d | 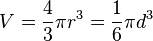 |
| พื้นที่ผิวของทรงกลมที่มีรัศมี r |  |
| ปริมาตรของทรงกระบอกที่สูง h และรัศมี r | 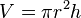 |
| พื้นที่ผิวของทรงกระบอกที่สูง h และรัศมี r |  |
| ปริมาตรของกรวยที่สูง h และรัศมี r | 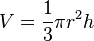 |
| พื้นที่ผิวของกรวยที่สูง h และรัศมี r |  |



